Advancements In Structural Optimization For Civil Engineering: A Comprehensive Literature Survey

Abstract

The architecture, engineering, and construction (AEC) industry is known for its intensive use of resources, making sustainability and efficiency essential goals in modern civil engineering. With rapid advancements in computational technologies, structural optimization has become a prominent method to enhance design performance while minimizing material use and cost. Although significant research has been conducted, a focused review of recent developments in this area remains limited. This paper aims to critically examine current research in structural optimization within civil engineering, highlighting key objectives, methods, and trends. After establishing the relevance of sustainable design in the AEC sector, the paper outlines the review methodology used to gather and analyze relevant academic literature. Articles are then assessed based on optimization goals, with attention to how these priorities have evolved over time and in different regions. The structural optimization process is broken down into four main stages: modeling and structural analysis, formulation of the optimization problem, applied optimization techniques, and computational tools or platforms. Each stage is discussed in detail using insights from selected studies. The review concludes by identifying knowledge gaps and offering suggestions for future research directions. By synthesizing current achievements and limitations, this paper provides a foundation for advancing structural optimization practices in sustainable civil engineering design.

Introduction

Civil engineering is a vital field focused on the planning, design, construction, and maintenance of infrastructure systems and built environments. This discipline encompasses a wide range of projects, including residential buildings, transportation networks like bridges and highways, and public utilities. Despite its essential role in societal development, the architecture, engineering, and construction (AEC) sector is frequently criticized for its low productivity, intensive labor requirements, and adverse environmental effects. The sector, while economically significant, also faces major challenges in improving sustainability and efficiency. Globally, the construction industry contributes substantially to the economy. According to Horta et al. [4], it accounts for nearly 9% of the world’s gross domestic product (GDP). In the context of energy consumption and emissions, the impact is even more significant. For instance, a study by Xu and Wang [5] revealed that in 2017, the construction sector was the second-largest consumer of energy in China. It was responsible for approximately 20% of the country’s total energy use, 23% of electricity consumption, and 30% of CO₂ emissions. These figures highlight the urgency of enhancing the environmental, social, and economic performance of civil engineering practices through innovative and sustainable solutions.

Over the past few decades, the integration of computational tools in structural engineering has opened new avenues for improving design processes. Among these, structural optimization—an approach grounded in mathematical modeling and computational algorithms—has gained significant traction. Structural optimization seeks to achieve the best possible configuration or design of a structure to meet specific performance goals under defined constraints. The increasing demand for efficient and sustainable designs has made optimization a central topic in civil engineering research and practice. Optimization, in general, refers to identifying the most effective solution to a problem given certain limitations or objectives. Within the civil engineering context, optimization techniques can be applied across the entire lifecycle of a project, including design, construction, operation, and maintenance. One particularly prominent area is structural optimization, which involves adjusting the geometric or topological characteristics of a structure to improve performance or reduce costs. In this paper, structural optimization is defined as the process of identifying the most effective arrangement of structural components to satisfy predefined design criteria, without delving into the properties of the materials used. Material choice is undeniably crucial in determining structural performance. Civil engineering structures often rely on concrete-based composite materials such as plain concrete, reinforced concrete, and prestressed concrete [1,9,10]. While multiple materials may be used in practice, optimization studies typically simplify analysis by focusing on structures composed of a single material. This simplification helps manage computational complexity, particularly in large-scale problems.

Structural optimization is a critical aspect of engineering design, broadly classified into four main categories: size, shape, topology, and multi-objective optimization. Size optimization focuses on altering the dimensions or cross-sectional areas of structural elements to enhance performance, typically aiming to reduce material usage while maintaining strength and stability. Shape optimization involves adjusting the geometry or nodal positions within the structure to achieve an improved and more efficient configuration, often leading to better stress distribution and overall functionality. Topology optimization, on the other hand, concerns the strategic arrangement of material within a given design space. It seeks to eliminate inefficient or redundant components, thereby creating lightweight structures without compromising performance. Lastly, multi-objective optimization integrates these approaches by simultaneously considering various objectives—such as minimizing weight, cost, and environmental impact—resulting in a comprehensive layout optimization strategy. This holistic method enables engineers to balance competing demands and achieve efficient, sustainable, and high-performing structural designs.

In earlier decades, structural optimization efforts were largely theoretical and confined to simple structures used as benchmark models. However, with the evolution of computational methods and advances in construction technology, these techniques are now applied to more complex and large-scale projects. For example, the Qatar National Convention Centre (QNCC) in Doha incorporated a three-dimensional evolutionary topology optimization algorithm known as Extended Evolutionary Structural Optimization (EESO) to minimize compliance and enhance structural performance [12]. Similarly, the Shenzhen CITIC Financial Center in China benefited from a topology-optimized exoskeleton truss system, which improved material efficiency without compromising structural stiffness [13].

One of the primary motivations behind structural optimization is cost reduction. Since structural components often represent a major portion of overall construction expenses, minimizing structural weight is a commonly pursued goal to reduce material usage and project cost [14]. Recently, the focus has expanded to include environmental considerations. The construction sector’s significant CO₂ emissions have driven researchers to develop optimization methods that not only minimize cost and weight but also aim to reduce environmental footprints. Furthermore, structural optimization has been used to enhance performance attributes such as mechanical behavior, seismic resistance, and aerodynamic stability [15], tailoring structures for diverse environmental conditions and functional demands. To meet these evolving goals, various optimization methods have been proposed and refined. Among them, metaheuristic algorithms—such as genetic algorithms, particle swarm optimization, and harmony search—have emerged as popular approaches for solving complex and high-dimensional problems [16]. These techniques are well-suited for combinatorial optimization and can explore large solution spaces effectively. However, they are not without drawbacks. Metaheuristics can be computationally intensive and may struggle with convergence in high-dimensional design spaces [17,18].

Consequently, recent studies have concentrated on enhancing the performance of these algorithms. For instance, Mortazavi [19] introduced a fuzzy decision-making enhancement to the Interactive Search Algorithm (ISA), resulting in the Fuzzy Tuned Interactive Search Algorithm (FTISA), which demonstrated improved computational efficiency and accuracy. Degertekin [20] developed improved versions of the harmony search algorithm—namely, the Efficient Harmony Search Algorithm and the Self-Adaptive Harmony Search Algorithm—for truss structure optimization. These methods delivered faster convergence and better results compared to the original approach. Likewise, Zheng et al. [21] introduced the Transformable Triangular Mesh (TTM) method, a novel explicit topology optimization technique, which outperformed many existing algorithms in terms of solution quality and computational speed.

Despite these advancements, the body of research remains fragmented, and there is a lack of comprehensive reviews that synthesize recent progress, identify trends, and outline future directions in structural optimization for civil engineering. This paper aims to fill that gap by providing a systematic and critical analysis of recent studies in the field. It explores optimization objectives, categorizes methodologies, assesses temporal and geographic research trends, and evaluates the optimization process across four key stages: structural modeling and analysis, problem formulation, optimization techniques, and computational platforms. The remainder of this paper is structured as follows. Section 2 describes the methodology used to collect and screen relevant literature. Section 3 provides statistical insights into the selected studies. Section 4 analyzes the optimization objectives and discusses how they have evolved over time and across regions. Section 5 offers a detailed review of the structural optimization process. Section 6 identifies research gaps and proposes future research directions. Finally, Section 7 concludes the paper with a summary of findings and implications for the field.

Methodology

This review employed a structured and systematic method to explore and synthesize current developments in structural optimization within civil engineering. The study’s process was divided into several interconnected phases, beginning with the identification and collection of relevant academic sources, followed by data categorization, statistical assessment, thematic analysis of optimization objectives, and a discussion of methodological trends, limitations, and future directions. An overview of the entire process is illustrated in Figure 1. The first step involved retrieving academic publications from a comprehensive online source—Google Scholar—due to its extensive database of peer-reviewed journals, conference proceedings, books, and theses. Details regarding the search procedure and selection criteria are discussed in Section 2.1. Section 2.2 provides a concise description of the keyword selection strategy.

 

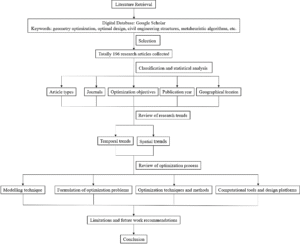
1.1 Literature Selection Process

Academic literature was sourced using Google Scholar, given its inclusive range of scholarly content. A set of targeted search terms was applied to identify publications focusing on various aspects of structural optimization. These terms encompassed concepts such as “size optimization,” “topology optimization,” “shape optimization,” “layout optimization,” “metaheuristic design,” and “civil engineering structures.” After obtaining search results, a manual screening process was carried out to select the most relevant and high-quality studies. A total of 196 works were chosen, comprising 154 journal papers, 19 conference contributions, 12 chapters from academic books, 7 literature reviews, and 4 doctoral theses. Although the concept of structural optimization dates back over a century, its application in civil engineering has gained traction primarily in recent decades, especially due to advances in computing. Therefore, the publication window for this review was set from 1970 to 2020 to ensure comprehensive coverage of both foundational and modern developments.

1.2 Keyword Identification Strategy

To ensure precise and inclusive literature coverage, keyword selection followed an iterative refinement process. Initial searches were conducted using broad terms like “civil engineering structural optimization.” From these, a number of recent review papers were analyzed to extract frequently used terminology in the field. This guided the inclusion of more specific keywords such as “topology optimization,” “metaheuristic algorithms,” and “optimal design.” The final list of keywords was designed to encompass the breadth of structural optimization techniques relevant to civil engineering.

Statistical Analysis of Selected Literature

An analysis of the temporal distribution of the selected literature was conducted, categorizing the publications across five distinct time intervals, as visualized in Figure 2. The results clearly show a notable upward trend in research activity over time. Specifically, 88% of the total articles were released post-2000, and an even larger portion—73%—were published after 2010. This pattern strongly reflects the growing academic interest and ongoing advancements in structural optimization research within civil engineering.

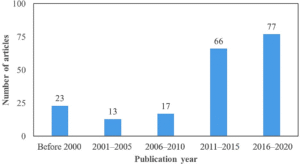
Figure 2: Distribution of the selected articles regarding the publication year.

To understand publication patterns across academic platforms, the sources of the selected works were examined. Figure 3 outlines the ten most frequently contributing journals. These top-tier journals collectively accounted for 82 of the total papers reviewed. Computers and Structures led the list with 21 contributions, followed by Structural and Multidisciplinary Optimization and Engineering Structures, each having published over 10 articles. This highlights the central role these journals play in disseminating cutting-edge research in this field.

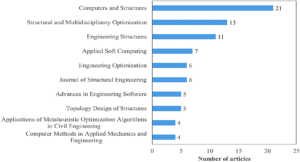
Figure 3. Number of selected articles published in the top ten journals.

Additionally, a geographical analysis was carried out based on the institutional affiliation of the first author. Figure 4 illustrates the regional distribution. Asia emerged as the leading contributor with 79 papers, while Europe and North America followed with 66 and 36 publications, respectively. Combined, these three continents produced 92% of the reviewed studies, underscoring the concentration of research output in these regions [22].

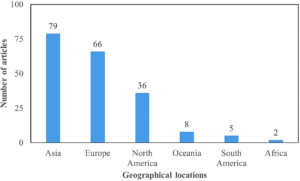
Figure 4: Distribution of selected articles by the continent of the first author’s research institution.

This statistical review provides a foundational understanding of research dissemination, highlighting both the rapid growth in scholarly interest and the leading platforms and regions contributing to the advancement of civil engineering structural optimization.

Purposes of Organizational Optimization

3.1  Classification of Optimization Goals

The reviewed literature on structural optimization in civil engineering reveals four principal categories of design goals:

1. Economic Efficiency – Aiming to reduce overall construction or material expenses, typically by minimizing structural weight or volume to lower costs.
2. Enhancement of Structural Capabilities – Focusing on improving functional attributes such as load resistance, vibration control, seismic durability, or aerodynamic efficiency, depending on environmental or usage requirements.
3. Eco-efficiency – Centered on minimizing ecological footprints through strategies that reduce energy usage or carbon emissions across the structure’s lifecycle.
4. Composite Objectives – Involving more than one goal from the categories above, often requiring a balance between cost, performance, and sustainability.

A detailed summary of these categories and associated key studies is provided in Table 1 for further reference and comparative assessment.

Optimization Objective	Description	Relevant Articles
Cost Minimization	Optimization for minimizing the total cost of civil engineering structures, usually achieved by reducing structure weight or volume.	Barbieri, Cinquini [23]; Lin, Che [24]; Zhou and Rozvany [25]; Liang, Xie [26]; Ghasemi and Dizangian [27]; Ho-Huu, Nguyen-Thoi [28]; Zhao, Xu [29]
Structural Performance Improvement	Optimization for improving certain properties of civil engineering structures to meet functional requirements.	Rahmatalla and Swan [30]; Natke and Soong [31]; Achtziger [32]; Wang [33]; Guest and Moen [34]; Uroš, Gidak [35]; Martin and Deierlein [36]
Environmental Impact Minimization	Optimization for reducing environmental impacts of civil engineering structures, such as greenhouse gas emissions and energy consumption.	Yi and Malkawi [37]; Brown and Mueller [38]; Penadés-Plà, García-Segura [39]; Mayencourt and Mueller [40]
Multi-objective Optimization	Optimization considering more than one of the above objectives, often combining cost, performance, and environmental factors.	Bremicker, Chirehdast [41]; Ohsaki and Swan [42]; Paik and Raich [43]; Munk, Vio [44]; Choi, Oh [3]; Xia, Langelaar [45]

An analysis of the selected articles reveals the distribution of structural optimization goals, as visualized in Figure 5. A significant proportion—62%—of the reviewed studies prioritizes minimizing project expenses. This often reflects the interests of stakeholders, particularly in terms of reducing the overall structural costs. A further 22% of the literature emphasizes enhancing structural capabilities, such as mechanical and dynamic resilience. Meanwhile, studies that simultaneously target multiple objectives, such as combining cost efficiency with performance gains, represent 14% of the articles. Only 2% of the literature focuses exclusively on reducing the ecological footprint of structures. One potential explanation is that strategies aimed at minimizing environmental impact, such as reducing embodied energy and carbon emissions, may inherently contribute to lower overall costs [39]. Consequently, these environmental considerations are more commonly embedded within multi-faceted optimization efforts, rather than pursued as standalone goals.

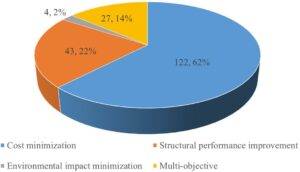
Figure 5: Number and proportion of articles for each optimization objective.

3.2   Temporal Evolution of Optimization Focus Areas

The field of structural optimization in civil engineering has grown steadily over the years, with noticeable shifts in research themes over time. To assess these changes, the distribution of articles across different optimization objectives is examined over five distinct time intervals, as depicted in Figures 6a and 6b. Prior to the year 2000, scholarly work in this area was largely concentrated on cost-saving approaches. Approximately 70% of the articles published in this early period targeted reductions in material quantity—either by minimizing structural volume or weight—as a means to lower construction expenses [46]. A smaller fraction of articles focused on enhancing structural behavior (17%) or tackled multiple objectives concurrently (13%). Within the early performance-focused literature, topology optimization was a widely used technique. This method involves removing underutilized elements from a design while meeting required constraints, thus optimizing system performance [31]. Despite the lack of standardization in performance criteria, several metrics were used in these studies, such as compliance [32,47], peak displacement, or maximum moment [48].

Regarding multi-objective studies, the earliest instances approached the problem by optimizing for different targets—such as compliance and weight—independently, before integrating these into a unified framework [41]. Some researchers addressed these trade-offs by converting multi-dimensional goals into single-objective problems using scalar multipliers [49], while others embraced Pareto-based methodologies to retain distinct objectives within a solution set [50]. In addition, after 2000, structural optimization research expanded considerably. The number of articles surged from 17 (2006–2010) to 66 (2011–2015), reflecting a growing scholarly interest. Throughout these later timeframes, cost minimization remained the dominant focus, although its relative proportion declined compared to the pre-2000 period. In the post-2000 periods, cost-related studies made up 54%, 59%, 67%, and 58% of the total articles in each respective interval. At the same time, interest in performance-based optimization also saw a steady rise, accounting for about 22% of all selected papers during this era.

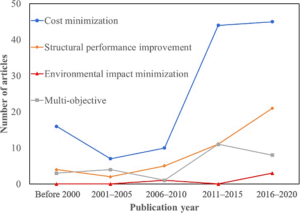
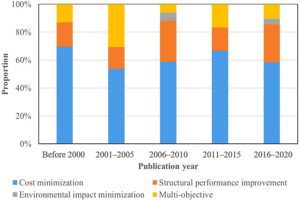
Figure 6: Number and proportion of articles with each objective in each time period: (a) number of articles, and (b) proportion of articles.

Studies centered on structural performance improvement gained relevance particularly in contexts where durability, safety, or seismic resistance were considered more crucial than simply reducing mass or cost [48]. Furthermore, multi-objective optimization continued to feature in the literature, though challenges such as computational intensity [50] and solution uncertainty [51] likely limited its broader adoption. This category constituted around 14% of the reviewed articles post-2000, and the number of such papers fluctuated across the analyzed periods. Interestingly, while sustainability-focused optimization remains underrepresented (2% of total articles), recent data shows increasing interest. Of the four studies focused solely on environmental impact, three were published between 2016 and 2020—suggesting that this subfield may experience growth in the future as environmental concerns gain prominence in structural engineering [39].

3.3   Regional Distribution of Optimization Themes

Research funding—whether sourced from governments or private entities—has a direct impact on the volume and focus of structural optimization studies across regions [52]. For the purpose of this geographical analysis, the articles were first classified by continent, following the “geographical scope” approach employed in prior reviews [53]. The analysis shows that Asia, Europe, and North America are the leading contributors to this field, which aligns with the data illustrated in Figure 5. Cost reduction appears to be the dominant focus in all three regions. However, in Europe and North America, the relative emphasis on cost is slightly lower compared to Asia. Notably, environmentally driven optimization objectives are represented only in European and North American research, while no such studies were found originating from Asia. Research output from other regions—namely Africa, South America, and Oceania—remains limited, with just two, five, and eight relevant publications, respectively. This suggests that structural optimization research is still in its infancy in these areas.

Further granularity is achieved by analyzing article contributions at the national level. Out of 196 collected papers, 37 countries were identified as contributors. Figure 8 highlights the top twelve countries in terms of research output. Iran, the United States, China, and Turkey are the most prolific, jointly accounting for 117 papers, or 60% of the total. In wealthier nations such as the United States, China, Australia, South Korea, Germany, Italy, Greece, Spain, and the United Kingdom, the objectives of optimization are more evenly distributed. These countries tend to invest in a balanced mix of cost efficiency, performance enhancement, and multi-objective strategies.

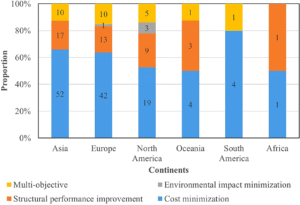
Figure 7: Distribution of articles with each objective in each continent.

In contrast, in countries with developing economies like Iran, Turkey, and Brazil, the research focus is largely centered around cost reduction—likely reflecting financial constraints and practical priorities. Additionally, countries located in earthquake-prone regions, including the USA, China, and South Korea, have shown greater interest in performance-focused optimization. This pattern suggests that local environmental conditions, such as seismic activity, influence the selection of structural optimization goals [10]. Researchers in these zones appear to be especially concerned with improving a structure’s resilience to dynamic forces and extreme conditions.

 

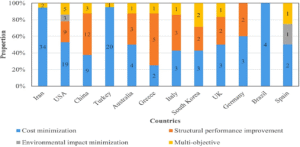
Figure 8: Distribution of articles with each objective in major countries.

Structural Optimization Process

In civil engineering, a variety of structural components such as beams, columns, and rods are subject to optimization; however, skeletal frameworks like trusses and frames represent the most commonly optimized structural forms. The optimization process involves several crucial elements that need to be addressed systematically. Initially, the modeling strategy employed for structural analysis and design forms the basis for classifying structural optimization into discrete and continuum approaches. Following that, the optimization problem must be precisely formulated by specifying the design variables, objective function(s), and any constraints. The choice of optimization technique—mathematical methods or programming algorithms—then plays a key role in effectively solving the problem. Finally, computational tools and design software platforms are essential for implementing these methods and conducting the design process. The upcoming subsections 5.1 and 5.2 explore these foundational aspects with reference to current literature and technological advancements.

4.1  Approaches to Structural Modeling and Design Analysis

Structural optimization is inherently iterative, requiring repeated evaluations of the structure to assess incremental improvements until an optimal design is achieved. Due to the high computational demand of this repetitive analysis, especially for complex large-scale structures, it is critical to employ analysis methods that are efficient in terms of computation time. The finite element method (FEM) is widely adopted for structural analysis, with simpler, coarse finite element models often favored over detailed models to reduce computational overhead. Another strategy involves simultaneous structural analysis and design integration, which streamlines the overall optimization process [22,54]. Based on the initial modeling technique, optimization can be divided into discrete optimization, where the structure is represented as distinct elements, and continuum optimization, which treats the structure as a continuous solid with variable topology. Discrete optimization is convenient for selecting cross-sectional sizes and nodal coordinates and is typically applied to size and shape optimization where the structural layout is predefined and fixed. This type of optimization is also referred to as non-topological or fixed-topology optimization, aiming to refine the shape or dimensions of the structure to improve performance criteria such as minimizing mass [1]. Representative examples of this approach can be found in studies [55–58]. In contrast, topology optimization often addresses connectivity and arrangement of structural elements to identify the best overall layout. Continuum optimization, which deals with material distribution within a solid domain, can potentially produce more innovative and efficient designs beyond typical truss or beam frameworks [42]. However, due to the increased complexity in problem formulation and programming challenges, continuum optimization remains less prevalent in civil engineering applications [47].

4.2   Defining the Structural Optimization Problem

The formulation of a structural optimization problem involves defining three essential components within the design search space: design variables, objective function(s), and constraints [10]. Design variables represent the adjustable parameters of the structural system, which may be continuous—able to take any value within a range—or discrete—limited to specific values. The objective function quantifies the goal of the optimization, such as minimizing weight or maximizing stiffness. Constraints impose essential limits and requirements for safety, serviceability, or other design standards, and these constraints can be expressed as either equality or inequality conditions. Notably, equality constraints can be converted into pairs of inequality constraints to accommodate different optimization techniques; for example, h(X) = 0 can be rewritten as h1(X) ≥ 0 and h2(X) ≤ 0 [22]. Additionally, constraints can be incorporated into the objective function using penalty functions, transforming constrained problems into unconstrained ones by penalizing infeasible solutions [59]. The search space is divided into feasible and infeasible domains, where feasible design points satisfy all constraints, and infeasible points violate one or more constraints. The overall optimization task is to find the design variables within the feasible domain that optimize the objective function while adhering to all constraints [56].

Minimize/Maximize :  f (X); Subject to : gi(X) ≤ 0, i = 1, 2, 3,, m;

hj(X) = 0, j = 1, 2, 3,   , p;

X ∈ S.

In structural optimization, the variable set typically comprises a vector X=[x1,x2,x3,…,xn] where n denotes the total number of design parameters. The optimization objective is symbolized as f(X), while gi(X) and hj(X) represent the inequality and equality constraints, respectively. Here, mmm and ppp correspond to the count of these constraints, and SSS defines the feasible design space. Structural optimization objectives can be broadly classified into four categories. The formulation of an optimization problem hinges on the goal being pursued. Establishing the objective function entails quantitatively defining the desired outcome within the confines of specific constraints. As a result, the representation of the objective may diverge from the actual target of the optimization effort. A frequently encountered objective in structural optimization is minimizing the overall cost, typically approximated through minimizing structural weight [60]. Consequently, optimizing for cost is often operationalized by seeking to reduce the total structural mass. This is because cost and weight are directly correlated in many contexts. However, some experts argue that weight alone does not provide an accurate estimate of cost, as lightweight structures can sometimes incur higher fabrication or material expenses [61]. Due to such discrepancies and the presence of uncertain parameters, few studies in civil engineering directly model cost as the objective function [46]. In size optimization problems, structural systems are generally segmented into components, each with a design variable that defines its cross-sectional area. This approach is based on the premise that the overall weight of a structure is dependent on these cross-sectional properties [60]. These models usually disregard variations in material distribution, allowing the objective function to be defined as follows [62]:

n

Minimize : W = ∑ γgA_i L_i

i=1

Here, the total weight WWW of the structure is computed as a function of the material density γ\gammaγ, gravitational acceleration g, design variables X={A1,A2,…,An} and the individual lengths Li​ of the structural elements. When it comes to shape optimization, the design variables are the coordinates of the nodes, and this technique is often coupled with size optimization for weight reduction [6,63,64]. In contrast, topology optimization focuses on determining the optimal configuration of connections between nodes, essentially deciding whether a structural element should exist between two points [65]. This process usually begins with an overly dense mesh of potential structural members, referred to as the “ground structure.” As optimization proceeds, redundant components are systematically eliminated, yielding a more efficient design [19]. Here, a binary vector is used to define the topology: a variable value of 1 indicates a removable element, while 0 marks an essential component [66]. Furthermore, topology optimization is often integrated with size optimization to further minimize weight. Structural components with near-zero cross-sectional areas are considered superfluous and thus excluded from the final design [66]. In cost-driven optimization tasks, it is common to incorporate constraints related to stress and displacement, in accordance with various regional or national design standards. These include ACI Codes for concrete structures, Eurocode 2, AASHTO standards, and British Standards [10]. Another objective in structural optimization is to enhance performance, which lacks a universally accepted quantifier. Instead, a variety of performance indicators such as stiffness [31], compliance [67], strain energy [68], and displacement under static loads [69] are used to model the objective function. Most studies seeking to enhance structural performance utilize topology optimization. This preference likely stems from the fact that topology optimization inherently seeks optimal distribution of material, which can subsequently be refined through shape or size adjustments [67]. In these cases, compliance minimization is typically employed to enhance structural stiffness. The objective function can be represented as follows [70]:

Minimize : C = F^T × u(x)

Here, C denotes structural compliance, FFF is the load vector applied to the structure, and u is the displacement vector. Compared to weight-centric optimization, performance optimization involves a more diverse set of constraints due to varying performance demands. For instance, to mitigate the effects of dynamic loading, natural frequency constraints are often applied [71]. Additional mechanical constraints such as stress limits, displacement bounds, stiffness thresholds, and buckling resistance are also used. Moreover, restrictions on material usage—either by volume or weight—are sometimes imposed to manage overall project cost [68]. A relatively underexplored goal in structural optimization is minimizing environmental impact. Only a limited number of studies address this aim. In such research, environmental impact is typically assessed based on metrics such as carbon emissions or embodied energy. Reducing material consumption is the primary method used to lower these environmental costs [39]. Similar to cost minimization, structural designs under this objective must also comply with conventional safety and serviceability constraints. In real-world civil engineering practice, there is an ongoing challenge to reduce costs while maximizing safety and functionality. These objectives often compete, meaning that gains in one area may lead to compromises in another [1]. To address this, many studies now explore multi-objective optimization techniques. These approaches seek to find a suitable balance between conflicting objectives, often focusing on two competing goals [72]. Multi-objective optimization distinguishes itself from single-objective methods by incorporating multiple target functions simultaneously. For instance, a study might aim to minimize both the weight and deflection of a structure [73]. Naturally, such problems are more computationally intensive and necessitate advanced solution strategies [72]. A key characteristic of multi-objective optimization is the absence of a single global optimum that satisfies all objectives equally. Instead, the solution set forms a Pareto front, representing various trade-offs among the objectives [74]. Mathematically, a multi-objective optimization problem can be framed as [1]:

Minimize the vector function

f(X) = [ f₁(X), f₂(X), f₃(X),      f_k(X)]^T

Subject to : g_i(X) ≥ 0, i = 1, 2, 3,        , m;

h_j(X) = 0, j = 1, 2, 3,   , p;

X ∈ S.

In multi-objective optimization, the goal is to identify a set of optimal trade-offs rather than a single best solution. The objective functions are denoted by f(X), while gi(X) and hj(X) represent the inequality and equality constraints, respectively. The variable vector X=[x1,x2,…,xn] spans the design space SSS. The outcome is a group of non-dominated solutions forming the Pareto optimal set, which, when plotted against performance criteria, generates the Pareto front [74]. This graphical representation supports informed trade-off decisions. Proper problem formulation defines variables, constraints, objectives, and the solution domain.

4.3   Optimization Techniques and Methods

Structural optimization has been one of the key focus areas within engineering research throughout the 20th century [75]. A landmark contribution in this domain was made by Kuhn and Tucker in 1951 [76], who laid the groundwork for mathematical programming approaches by introducing essential techniques such as the Lagrange multipliers and the equivalence theorem. These foundational concepts significantly influenced the development of optimization methodologies over the years. More recently, both mathematical programming and computational search methods have become the predominant strategies employed for efficiently locating optimal design solutions in structural systems. Typically, the optimization process initiates with an initial guess and iteratively adjusts the design to enhance the objective function until convergence is met [22].

In structural optimization within civil engineering, two principal classes of methods are commonly adopted: gradient-based strategies and heuristic-based algorithms [61]. Gradient-based methods utilize directional information, referred to as gradients, to navigate the design space toward optimality. These techniques are generally categorized into four groups: linear programming, non-linear programming, optimality criteria, and feasible direction methods [61]. Linear programming applies when both the objective function and constraints are linear, while non-linear programming is used if any function is non-linear. Optimality criteria methods create specialized algorithms that optimize structures under constraints like stiffness, often relying on structural mechanic’s theories [77]. These methods frequently involve computing Lagrange multipliers, which help identify local extrema under equality constraints, including stress and displacement limitations. Feasible direction methods, on the other hand, start from a point that complies with all constraints and advance in a direction that both respects the constraints and reduces the objective function.

X_i+1 = X_i + λS_i

The movement from point Xi​ to Xi is guided by a direction vector Si and a predefined step length λ, ensuring the new point remains feasible. The direction Si​ must allow improvement without violating constraints, and it must contribute to decreasing the objective function [78]. To manage computational expense, approximation techniques are often integrated into gradient-based optimization. These approximations initially simplify the problem through analysis and are then refined using optimization procedures. The resulting solution is used to inform subsequent design iterations [22]. These traditional methods, often referred to as classical or conventional approaches, played a vital role in early civil engineering applications. For instance, Chan [6] utilized linear programming for multi-load structural optimization, while Dobbs and Felton [79] applied a steepest descent method to optimize truss geometries. Lin et al. [24] developed the α-β bi-factor iterative method, classified under feasible direction methods, to achieve weight reduction under dynamic and static load conditions. Nevertheless, several studies have noted important limitations in these techniques, which generally fall into three categories.

In the context of civil engineering structural optimization, gradient-based methods have historically demonstrated competent performance in specific scenarios. However, their effectiveness in achieving a global optimum is often questioned due to inherent limitations. These techniques are highly sensitive to the initial design configuration and the direction of the search, commonly known as the gradient. Consequently, in problems with multiple local optima—a common scenario in structural optimization—these methods are prone to settling at suboptimal solutions rather than exploring the entire design space to reach a true global optimum [6]. This tendency to become confined within local optima reflects a significant drawback, particularly when complex structural systems with intricate design landscapes are involved.n Moreover, these approaches necessitate the computation of gradient information, which often involves analytical derivatives or computationally intensive numerical approximations. This requirement significantly complicates their application in cases where constraints are highly nonlinear, non-differentiable, or discontinuous [80]. For large-scale or real-world engineering problems, where constraint relationships are rarely simple or linear, the computational burden becomes substantial, thereby reducing the practical feasibility of using gradient-based approaches. Furthermore, these algorithms tend to offer limited flexibility in handling comprehensive and realistic sets of design constraints. Most are tailored to specific types of problems and lack the adaptability required to encompass the full spectrum of engineering constraints encountered in advanced structural optimization cases [6].

To overcome these challenges, a new category of solution strategies known as heuristic methods has emerged. Heuristic algorithms are based on intelligent guesswork and problem-specific rules rather than exact mathematical formulations. They often incorporate learning-based approaches, such as artificial neural networks [81] and support vector machines [82], which iteratively refine solutions through feedback mechanisms [83]. While these methods are generally more intuitive to implement and capable of handling complex systems more efficiently, they too face certain limitations. Notably, their performance can be highly problem-dependent, and without mechanisms to escape local optima, they might fail to locate global solutions in non-convex design spaces [84]. To address these shortcomings, researchers have advanced a more generalized class of optimization strategies known as metaheuristic algorithms. Unlike traditional heuristics, metaheuristics are typically problem-independent and incorporate stochastic elements that enable broader exploration of the design space. They effectively balance local refinement and global search capabilities by combining randomization with directed search strategies [83]. These methods draw inspiration from natural and artificial processes, such as biological evolution, swarm intelligence, musical improvisation, and collective behavior. Examples include genetic algorithms (GA) [85], harmony search (HS) [86], firefly algorithm (FA) [87], artificial bee colony (ABC) [88], differential evolution (DE) [89], Tabu search (TS) [90], teaching–learning-based optimization (TLBO) [91], particle swarm optimization (PSO) [92], bat algorithm (BA) [93], cuckoo search (CS) [94], and the Jaya algorithm [95]. Metaheuristics are commonly categorized based on their inspiration source (nature-based vs. non-nature-based), population strategy (individual vs. group-based), and adaptability to changing objective functions (static vs. dynamic) [96].

Despite their diverse origins, all metaheuristic methods typically share two critical mechanisms: exploration and exploitation [16]. Exploration allows algorithms to sample broadly across the design space, ensuring solution diversity, while exploitation refines promising solutions to converge toward optima. An effective interplay between these two elements is crucial to avoid premature convergence and ensure robustness across a wide range of structural optimization problems. Metaheuristic algorithms offer several advantages over traditional methods. Firstly, they are adept at addressing combinatorial problems involving both discrete and continuous variables. Secondly, they circumvent the need for gradient information, which simplifies their application in highly nonlinear or implicit constraint scenarios. Thirdly, metaheuristics operate effectively without requiring explicit convexity or analytical relationships between design variables and constraints. Lastly, they are often more capable of identifying global optima, making them particularly valuable in complex structural optimization [16]. These benefits have led to numerous successful implementations in the field. For instance, Kociecki and Adeli [97] developed a two-stage GA to optimize the size and layout of frame structures, reducing weight while considering topological constraints. Similarly, Mortazavi and Toğan [71] integrated PSO into truss structure optimization to enhance dynamic performance and reduce weight. Bekdaş et al. [62] demonstrated the utility of the flower pollination algorithm in achieving size optimization in trusses.

Nevertheless, metaheuristics are not without drawbacks. As noted by Sörensen [17], many metaheuristic algorithms involve complex mechanisms and have only been tested on relatively small problem instances, raising questions about their general applicability to large-scale structures. While they can deliver excellent results in controlled settings, this does not guarantee superior performance over more traditional constructive heuristics. Furthermore, Saka et al. [16] argue that the computational demands of metaheuristics can be substantial, particularly for complex problems involving numerous loading scenarios. Mahdavi et al. [18] also highlight that standard metaheuristics often struggle with high-dimensional design spaces due to the vast and intricate nature of such landscapes, which impairs their ability to efficiently explore and optimize. As a result, recent advancements have focused on improving existing metaheuristic algorithms. These enhancements typically aim to boost efficiency and accuracy by leveraging the specific strengths of each method. For example, Cheng et al. [98] introduced a hybrid version of HS that integrates PSO’s search capabilities and localized neighborhood exploration, replacing the original algorithm’s randomization elements while preserving its key memory and adjustment features. This modified approach achieved superior convergence rates and solution precision. Arjmand et al. [99] developed another hybrid model by combining an enhanced dolphin echolocation algorithm with ant colony optimization, capitalizing on the strengths of both to enhance solution efficiency. Cao et al. [100] also proposed four distinct ways to improve PSO: optimizing the balance between global and local searches, modifying the algorithm’s topology structure, merging it with other metaheuristics, and integrating it with classical gradient-based methods. These adaptations improve both the breadth of search and convergence speed while minimizing error margins.

Apart from algorithmic improvements, another strategy to enhance optimization efficiency is to minimize the frequency and complexity of objective or constraint evaluations during the optimization cycle. However, as Cao et al. [100] caution, this may lead to results that deviate from intended objectives and compromise design integrity, and thus this approach is not further elaborated in this work. Finally, beyond gradient-based and heuristic/metaheuristic techniques, another class of optimization approach exists—reliability-based design optimization (RBDO). These methods incorporate uncertainties in design variables, material properties, load conditions, and structural behavior to achieve an optimal trade-off between performance and reliability [101]. RBDO ensures minimum safety thresholds are met, providing engineers with probabilistic assurances during design [102]. The primary RBDO strategies include the two-level, single-loop, and decoupled approaches [101]. Despite their appeal, the practical application of RBDO in civil engineering remains constrained by challenges such as high computational demand due to repetitive reliability assessments and the difficulty in computing probabilistic constraint gradients [103].

A summary of some recently proposed improved metaheuristic algorithms is presented in table 2:

Year	Involved Algorithms	Inspiration / Description	Reference
2012	Efficient Harmony Search (EHS) and Self-Adaptive Harmony Search (SAHS)	Proposed improved HS algorithms to reduce parameter dependency and enhance exploitation and exploration capacities for size optimization.	Degertekin [20]
2016	Enhanced GA with Multiple Populations (EGAwMP)	Combined GA with multiple populations, radial-basis neural network, and a new design strategy to increase convergence of optimal designs.	TALASLIOGLU [104]
2017	Accelerated Firefly Algorithm (AFA)	Improved standard firefly algorithm by reducing randomness and scaling random term to increase convergence rate.	Baghlani, Makiabadi [105]
2017	Improved Ray Optimization (IRO)	Modified solution generation and applied feasibility enforcement to enhance original ray optimization efficiency.	Kaveh and Ghazaan [106]
2017	Hybrid GA and PSO (HGAPSO)	Divided population based on fitness; PSO used for better half, GA for worse half to improve search capability.	Maheri, Askarian [107]
2017	Colliding Bodies Optimization (CBO) and Enhanced CBO (ECBO)	CBO based on one-dimensional collision; ECBO adds memory for performance improvement without extra computational cost.	Kaveh and Moradveisi [108]
2017	Integrated Particle Swarm Optimization (IPSO)	Combined PSO with improved fly-back mechanism and weighted particles for structural weight minimization under frequency constraints.	Mortazavi and Togan [71]
2017	Genetic Algorithm with Domain Trimming (GADT)	Enhanced GA with domain-trimming to improve global search capacity; applied to design of offshore wind turbine support structures.	AlHamaydeh, Barakat [109]
2017	Whale Optimization Algorithm (WOA) and Enhanced WOA (EWOA)	Inspired by whale hunting behavior; EWOA improves accuracy, reliability, and convergence rate over standard WOA.	Kaveh [110]
2017	Adaptive Hybrid Evolutionary Firefly Algorithm (AHEFA)	Automatically adapts parameters for effective global-local search trade-off; uses elitist selection to retain best individuals.	Lieu, Do [64]
2017	Discrete Advanced Jaya Algorithm (DAJA)	Generates new trial designs with descent directions; overcomes lack of parameter tuning in original Jaya algorithm.	Degertekin, Lamberti [66]

4.4    Computational Tools and Design Platforms

The advancement of computational technologies has significantly transformed how structural optimization is conducted, shifting from laborious manual calculations to streamlined, software-based solutions. Previously, structural design and analysis relied heavily on trial-and-error approaches, which were not only time-consuming but also highly susceptible to mistakes. With the evolution of digital tools, engineers now have access to sophisticated platforms that facilitate modeling, analysis, and optimization. Popular applications such as SAP2000 and ETABS have become widely adopted due to their enhanced computational speed and accuracy, delivering more reliable outcomes for various structural configurations [111]. However, these advantages are not universal across all platforms. Certain tools demonstrate limited capability when applied to large-scale or complex structural systems, resulting in reduced efficiency [10]. Similarly, software grounded in building information modeling (BIM) principles often encounters challenges related to low interoperability, which can hinder seamless data exchange between programs [112]. In structural optimization workflows, the choice of software is a crucial factor influencing both accuracy and computational performance. Once the problem and optimization strategy are clearly defined, the next stages typically include solution encoding, numerical computation, and design validation. The encoding of design variables—either in binary or real-number formats—depends largely on the nature of the selected metaheuristic algorithm [1].

Optimization tasks generally require two categories of software: one to execute the optimization algorithms and another to manage structural modeling and design. The computational program generates candidate solutions in iterative cycles, with each cycle producing new sets of design variable values. These variables are then imported into the design software to update the model’s geometry. Upon achieving convergence, designers identify the optimal solution by examining the feasible range of design variables through structural analysis based on pre-established criteria [113]. MATLAB remains a preferred computational tool in this domain due to its robust programming and numerical processing capabilities. Several notable applications underscore this point: Zhou et al. [114] developed a modified BESO approach using MATLAB, and Zegard and Paulino [115] created GRAND3—a MATLAB-based tool—for applying the ground structure method in 3D topology optimization. In practice, design software like ETABS, SAP2000, or ANSYS is typically used to carry out structural analysis, with BIM platforms often requiring data translation before integration with finite element analysis tools [10]. More recently, efforts have been made to streamline the entire optimization cycle within a single platform. For instance, Sotiropoulos and Lagaros [113] constructed an integrated system where SAP2000 directly interfaces with MATLAB’s fmincon function, eliminating the need for separate software or data conversion steps. Despite limited coverage in existing literature, computational environments and platforms are vital to achieving optimal structural designs. While current tools are generally effective, there remains a strong demand for more integrated and high-performance systems to enhance computational efficiency and ensure better data compatibility.

Limitations and Future Research Directions

In recent decades, advancements in theoretical approaches and computational techniques have significantly driven progress in structural optimization within civil engineering. Structural optimization today spans various dimensions, including the size, shape, and topology of structural systems. Objectives have diversified, ranging from cost reduction and improved mechanical performance to minimizing environmental footprint and addressing multiple goals simultaneously. Furthermore, the adoption of metaheuristic algorithms has greatly enhanced the optimization process in terms of precision and computational efficiency. Despite this progress, several challenges and unresolved issues remain. This section outlines the principal limitations and suggests directions for future investigations.

5.1   Weighting Strategies in Multi-Objective Optimization

As previously highlighted, multi-objective optimization (MOO) has become a vital focus within civil engineering, enabling trade-offs among competing goals to meet diverse design requirements. However, challenges persist. MOO problems typically yield a set of non-dominated solutions known as the Pareto front, but choosing the most appropriate solution from this set remains difficult. Additionally, all reviewed studies have only addressed dual-objective scenarios; optimization involving three or more objectives has yet to be fully explored. Several strategies have been developed to tackle the limitations of Pareto-based optimization. One such method is the compromise solution approach, which introduces a theoretical ideal point and aims to minimize the deviation from this target [116]. Nonetheless, this approach requires dimensionless objectives to assess proximity accurately, which is not always feasible [116].

Another prevalent strategy involves incorporating the preferences of stakeholders via weighting schemes. Depending on when the preferences are introduced, these methods are categorized into three types: a priori, interactive, and a posteriori [117]. In a priori methods, weights are assigned to each objective before optimization begins. Common techniques under this category include the linearly weighted sum method [118], the global criterion method [116], and scalar performance-based criteria [119]. For example, Sanaei and Babaei [120] applied the weighted sum approach to perform simultaneous shape and topology optimization. This technique transforms a multi-objective problem into a single-objective one using weighted coefficients for each goal. Interactive approaches gather input during the optimization process, though their use in structural optimization is limited due to the potential inconsistency in human judgment [117]. On the other hand, a posteriori approaches incorporate preferences after the Pareto set is generated. For instance, Zavala et al. [1] employed this method by approximating the Pareto front first, and then refining the solution based on user input.

Despite these efforts, weighting methods remain inherently subjective. Selecting appropriate weights often depends on decision-makers’ intuition, which can vary widely across projects. Moreover, not all stakeholders are capable of expressing clear preferences, particularly when facing trade-offs between conflicting goals [116]. Future research should aim to establish a robust framework for assigning weights in structural optimization. This framework could offer recommended weight ranges tailored to specific algorithms, structural codes, and constraints, helping practitioners choose suitable parameters even in the absence of clear preferences. Such a system would also support problems with more than two objectives, allowing them to be treated within a unified optimization framework.

5.2   Challenges in Objective Quantification

To achieve optimal solutions, structural objectives must be translated into quantifiable metrics. Common metrics include weight for cost estimation, and compliance or strain energy for evaluating stiffness. In principle, any structural characteristic, including aesthetics, can be optimized if appropriately measured [121]. However, translating some objectives into numerical form remains problematic. As Aldwaik and Adeli [61] noted, structural weight does not comprehensively reflect total cost. While lighter structures may lower material expenses, they may not fully account for transportation, labor, and installation costs. For example, Kaveh [122] proposed a more detailed cost model incorporating fabrication time, weight, and web cutting costs for optimizing castellated beams. Sharafi et al. [123] combined material and formwork costs in reinforced concrete beam design.

Parametric mixed-integer nonlinear programming (MINLP) has also been adopted to handle both continuous and discrete variables in structural cost optimization [124–126]. Algorithms such as the outer approximation/equality relaxation (OA/ER) and generalized Benders decomposition (GBD) [127] are commonly applied. These methods allow various factors—material unit prices, labor wages, imposed loads, and structural spans—to be integrated into one objective function. However, MINLP models are computationally intensive due to their nonlinear and combinatorial nature, limiting their widespread use [127]. To address this, future studies should focus on developing standardized cost estimation systems. These systems should incorporate comprehensive datasets covering material, labor, transportation, and construction methods (e.g., precast vs. cast-in-place), along with component standardization. Additionally, better models are needed for capturing mechanical and aesthetic performance, enabling these factors to serve as meaningful optimization objectives.

5.3   Generalizability of Optimization Algorithms

Many studies aim to develop optimization algorithms with improved convergence and performance. However, a unified benchmarking framework for comparing algorithm efficiency and robustness is lacking. For instance, Kaveh et al. [128] compared seven metaheuristic algorithms across three steel frame configurations. Performance rankings varied between cases, and no single algorithm consistently outperformed others. Convergence behavior also differed, with TEO, TLBO, and WEO often showing faster convergence, albeit inconsistently. These variations reveal that algorithm performance is context-dependent. An algorithm optimized for one structural configuration may not perform well on another. Moreover, the lack of standardized test cases hampers objective comparisons between newly developed algorithms. Consequently, future research should focus on creating a benchmarking platform for algorithm validation. Structural optimization tasks could be categorized by structure type, scale, or complexity. Within each category, standard problems and reference algorithms should be defined. This would allow consistent evaluation of new algorithms by comparing their performance against known baselines. Ultimately, such a framework would drive the development of more versatile and reliable optimization tools.

Conclusion

This review thoroughly examined the existing body of literature on structural optimization within civil engineering. A total of 196 pertinent articles were gathered from Google Scholar, spanning from 1970 through 2020. These papers were subjected to statistical analysis focusing on publication year, article type, journal distribution, geographical origins, and the primary goals of optimization. Trends over time and across different regions were carefully evaluated, revealing a steady increase in research output, particularly in countries with strong governmental funding support. Among various optimization aims, cost reduction remains the dominant focus; however, recent years have seen a rapid rise in studies targeting enhancements in structural performance and multi-objective optimization approaches. The review further detailed the structural optimization procedure by categorizing the collected works into four key thematic areas: minimizing costs, improving structural behavior, reducing environmental impacts, and multi-objective optimization. The process itself involves four fundamental phases: structural analysis and modeling, optimization problem formulation, choice of optimization techniques, and the utilization of computational platforms and software tools. Initial modeling approaches typically fall into two categories—discrete and continuum optimization. Formulating the optimization problem includes identifying design variables (such as cross-sectional dimensions, node coordinates, and element connectivity), objective functions (like minimizing total weight or strain energy), and constraints that ensure safety and serviceability, including stress limits and allowable displacements. Metaheuristic algorithms, grounded in mathematical programming, have gained prominence for delivering improved convergence speeds and solution accuracy compared to traditional methods, with many studies focusing on developing new or enhanced algorithms.

In terms of implementation, optimization methods are integrated within computing environments such as MATLAB for iterative solution finding, and the resulting designs are often evaluated using structural design software like ETABS. Some integrated platforms streamline this process by eliminating the need for data transfer between tools. Despite these advancements, current research still faces notable limitations. Key challenges include establishing weighting methods to transform multi-objective optimization problems into single-objective ones, developing standardized metrics for accurately quantifying optimization goals, and improving the generalizability of metaheuristic algorithms. The latter is important because algorithm performance varies with different problem types, highlighting the need for problem classification and benchmark systems to guide future algorithm development. In summary, this article contributes significantly by offering a comprehensive overview of civil engineering structural optimization research, analyzing publication patterns over time and space, explaining the core components of the optimization process, and identifying research gaps while suggesting future directions. It addresses the deficiency of a detailed review in this domain and provides valuable insights for advancing structural optimization studies.

Author Contributions: Conceptualization, L.M. and Q.W.; methodology, L.M. and Q.W; writing— original draft preparation, L.M.; writing—review and editing, Q.W. All authors have read and agreed to the published version of the manuscript.

Funding: This research was funded by Singapore Ministry of Education, grant number R-296-000- 213-114

Institutional Review Board Statement: Not applicable.

Informed Consent Statement: Not applicable.

Data Availability Statement: No new data were created or analyzed in this study. Data sharing is not applicable to this article.

Conflicts of Interest: The authors declare that they have no conflict of interest.

References

1. Zavala, G.R.; Nebro, A.J.; Luna, F.; Coello, C.A.C. A survey of multi-objective metaheuristics applied to structural optimization. Multidiscip. Optim. 2014, 49, 537–558. [CrossRef]
2. Kazaz, A.; Ulubeyli, S. Physical factors affecting productivity of Turkish construction workers. In Proceedings of the 22nd Annual ARCOM Conference, Birmingham, UK, 4–6 September 2006.
3. Choi, S.W.; Oh, B.K.; Park, H.S. Design technology based on resizing method for reduction of costs and carbon dioxide emissions of high-rise buildings. Energy Build. 2017, 138, 612–620. [CrossRef]
4. Horta, I.M.; Camanho, A.S.; Johnes, J.; Johnes, G. Performance trends in the construction industry worldwide: An overview of the turn of the century. Product. Anal. 2013, 39, 89–99. [CrossRef]
5. Xu, G.; Wang, W. China’s energy consumption in construction and building sectors: An outlook to 2100. Energy 2020, 195, 117045. [CrossRef]
6. Topping, B. Shape optimization of skeletal structures: A review. Struct. Eng. 1983, 109, 1933–1951. [CrossRef]
7. Rajput, S.P.; Datta, S. A review on optimization techniques used in civil engineering material and structure design. Today Proc. 2020, 26, 1482–1491. [CrossRef]
8. Tsiptsis, I.N.; Liimatainen, L.; Kotnik, T.; Niiranen, J. Structural optimization employing isogeometric tools in Particle Swarm J. Build. Eng. 2019, 24, 100761. [CrossRef]
9. Gagg, C.R. Cement and concrete as an engineering material: An historic appraisal and case study analysis. Fail. Anal. 2014, 40, 114–140. [CrossRef]
10. Afzal, M.; Liu, Y.; Cheng, J.C.; Gan, V.J. Reinforced concrete structural design optimization: A critical review. Clean. Prod. 2020, 260, 120623. [CrossRef]
11. Xiao, A.; Wang, B.; Jin, Y. Evolutionary truss layout optimization using the vectorized structure approach. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancún, Mexico, 20–23 June 2013.
12. Białkowski, S. Structural optimisation methods as a new toolset for architects. In Proceedings of the 34th eCAADe Conference— Complexity & Simplicity, Oulu, Finland, 24–26 August
13. Sun, Nonlinear Analysis of Topology-Optimized Scissor-Like Elements during Deployment and Structural Performance Analysis; Massachusetts Institute of Technology: Cambridge, MA, USA, 2020.
14. Kaveh, A.; Khayatazad, M. Ray optimization for size and shape optimization of truss structures. Struct. 2013, 117, 82–94. [CrossRef]
15. Tian, X.; Wang, Q.; Liu, G.; Liu, Y.; Xie, Y.; Deng, W. Topology optimization design for offshore platform jacket structure. Ocean Res. 2019, 84, 38–50. [CrossRef]
16. Saka, P.; Hasançebi, O.; Geem, Z.W. Metaheuristics in structural optimization and discussions on harmony search algorithm. Swarm Evol. Comput. 2016, 28, 88–97. [CrossRef]
17. Sörensen, Metaheuristics—The metaphor exposed. Int. Trans. Oper. Res. 2015, 22, 3–18. [CrossRef]
18. Mahdavi, S.; Shiri, M.E.; Rahnamayan, S. Metaheuristics in large-scale global continues optimization: A survey. Inf Sci. 2015, 295, 407–428. [CrossRef]
19. Mortazavi, A new fuzzy strategy for size and topology optimization of truss structures. Appl. Soft Comput. 2020, 93, 106412. [CrossRef]
20. Degertekin, S. Improved harmony search algorithms for sizing optimization of truss structures. Struct. 2012, 92, 229–241. [CrossRef]
21. Zheng, ; Tang, W.; Li, B. A new topology optimization framework for stiffness design of beam structures based on the transformable triangular mesh algorithm. Thin Walled Struct. 2020, 154, 106831. [CrossRef]
22. Haftka, T.; Gürdal, Z. Elements of Structural Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012; Volume 11.
23. Barbieri, ; Cinquini, C.; Lombard, M. Shape/size optimization of truss structures using non-probabilistic description of uncertainty. WIT Trans. Built Environ. 1970, 31, 1–10.
24. Lin, J.; Che, W.; Yu, Y. Structural optimization on geometrical configuration and element sizing with statical and dynamical Comput. Struct. 1982, 15, 507–515. [CrossRef]
25. Zhou, ; Rozvany, G. The COC algorithm, Part II: Topological, geometrical and generalized shape optimization. Comput. Methods Appl. Mech. Eng. 1991, 89, 309–336. [CrossRef]
26. Liang, Q.; Xie, Y.M.; Steven, G.P. Topology Optimization of Strut-and-Tie Models in Reinforced Concrete Structures Using an Evolutionary Procedure; American Concrete Institute: Farmington Hills, MI, USA, 2000.
27. Ghasemi, M.R.; Dizangian, B. Size, shape and topology optimization of composite steel box girders using pso method. Asian Civ. Eng. Build. Hous. 2010, 11, 699–715.
28. Ho-Huu, ; Nguyen-Thoi, T.; Nguyen-Thoi, M.H.; Le-Anh, L. An improved constrained differential evolution using discrete variables (D-ICDE) for layout optimization of truss structures. Expert Syst. Appl. 2015, 42, 7057–7069. [CrossRef]
29. Zhao, ; Xu, B.; Han, Y.; Rong, J. Continuum structural topological optimization with dynamic stress response constraints. Adv. Eng. Softw. 2020, 148, 102834. [CrossRef]
30. Rahmatalla, S.; Swan, C.C. Form finding of sparse structures with continuum topology optimization. Struct. Eng. 2003, 129, 1707–1716. [CrossRef]
31. Natke, ; Soong, T. Topological structural optimization under dynamic loads. WIT Trans. Built Environ. 1970, 2, 67–78.
32. Achtziger, W. Minimax compliance truss topology subject to multiple loading. In Topology Design of Structures; Springer: Berlin/Heidelberg, Germany, 1993; pp. 43–54.
33. Wang, D. Optimal shape design of a frame structure for minimization of maximum bending moment. Struct. 2007, 29, 1824–1832. [CrossRef]
34. Guest, K.; Moen, C.D. Reinforced concrete design with topology optimization. In Proceedings of the Structures Congress 2010: 19th Analysis and Computation Specialty Conference, Orlando, FL, USA, 12–15 May 2010.
35. Uroš, M.; Gidak, P.; Lazarevic´, D. Optimization of stadium roof structure using force density method. In Proceedings of the Third International Conference on Structures and Architecture (ICSA2016)-Structures and Architecture-Beyond Their Limits, Guimaraes, Portugal, 27–29 July 2016; Cruz, P.J.S., Ed.; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2016.
36. Martin, A.; Deierlein, G.G. Structural topology optimization of tall buildings for dynamic seismic excitation using modal Eng. Struct. 2020, 216, 110717. [CrossRef]
37. Yi, K.; Malkawi, A.M. Optimizing building form for energy performance based on hierarchical geometry relation. Autom. Constr. 2009, 18, 825–833. [CrossRef]
38. Brown, C.; Mueller, C.T. Design for structural and energy performance of long span buildings using geometric multi-objective optimization. Energy Build. 2016, 127, 748–761. [CrossRef]
39. Penadés-Plà, V.; García-Segura, T.; Yepes, V. Accelerated optimization method for low-embodied energy concrete box-girder bridge design. Struct. 2019, 179, 556–565. [CrossRef]
40. Mayencourt, P.; Mueller, C. Hybrid analytical and computational optimization methodology for structural shaping: Material- efficient mass timber Eng. Struct. 2020, 215, 110532. [CrossRef]
41. Bremicker, ; Chirehdast, M.; Kikuchi, N.; Papalambros, P.Y. Integrated topology and shape optimization in structural design. J. Struct. Mech. 1991, 19, 551–587. [CrossRef]
42. Ohsaki, M.; Swan, C. Topology and geometry optimization of trusses and frames. Recent Adv. Optim. Struct. Des. 2002, 5, 97–123.
43. Paik, S.; Raich, A. Development of a computational method for simultaneous optimization in an unstructured design domain. Int. Conf. Comput. Decis. Mak. Civil Build. Engr. 2006, 1644–1653.
44. Munk, D.J.; Vio, G.A.; Steven, G.P. Topology and shape optimization methods using evolutionary algorithms: A review. Struct. Multidiscip. Optim. 2015, 52, 613–631. [CrossRef]
45. Xia, Y.; Langelaar, M.; Hendriks, M.A. Automated optimization-based generation and quantitative evaluation of Strut-and-Tie models. Comput. Struct. 2020, 238, 106297. [CrossRef]
46. Sarma, K.C.; Adeli, H. Cost optimization of concrete structures. J. Struct. Eng. 1998, 124, 570–578. [CrossRef]
47. Mijar, A.R.; Swan, C.C.; Arora, J.S.; Kosaka, I. Continuum topology optimization for concept design of frame bracing systems. J. Struct. Eng. 1998, 124, 541–550. [CrossRef]
48. Imam, M.; Al-Shihri, M. Optimum topology of structural supports. Comput. Struct. 1996, 61, 147–154. [CrossRef]
49. Allaire, G.; Kohn, R. Topology optimization and optimal shape design using homogenization. In Topology Design of Structures; Springer: Berlin/Heidelberg, Germany, 1993; pp. 207–218.
50. Simões, L.; Negrão, J. Sizing and geometry optimization of cable-stayed bridges. Comput. Struct. 1994, 52, 309–321. [CrossRef]
51. Ruy, W.S.; Yang, Y.S.; Kim, G.H.; Yeun, Y.S. Topology design of truss structures in a multicriteria environment. Comput. Aided Civil Infrastruct. Eng. 2001, 16, 246–258. [CrossRef]
52. Olawumi, T.O.; Chan, D.W.M.; Wong, J.K.W. Evolution in the intellectual structure of BIM research: A bibliometric analysis. J. Civil Eng. Manag. 2017, 23, 1060–1081. [CrossRef]
53. De Castro e Silva Neto, D.; Cruz, C.O.; Rodrigues, F.; Silva, P. Bibliometric analysis of PPP and PFI literature: Overview of 25 years of research. J. Constr. Eng. Manag. 2016, 142, 06016002. [CrossRef]
54. Wu, C.; Arora, J. Simultaneous analysis and design optimization of nonlinear response. Eng. Comput. 1987, 2, 53–63. [CrossRef]
55. Grzywin´ski, M. Size and Shape Design Optimization of Truss Structures Using the Jaya Algorithm. Comput. Assist. Methods Eng. Sci. 2020, 27, 177–184.
56. Darvishi, P.; Shojaee, S. Size and Geometry Optimization of Truss Structures Using the Combination of Dna Computing Algorithm and Generalized Convex Approximation Method. Int. J. Optim. Civil Eng. 2018, 8, 625–656.
57. Kaveh, A.; Kalatjari, V. Size/geometry optimization of trusses by the force method and genetic algorithm. ZAMM J. Appl. Math. Mech. Z. Angew. Math. Mech. Appl. Math. Mech. 2004, 84, 347–357. [CrossRef]
58. Cheng, W.; Liu, F.; Li, L. Size and geometry optimization of Trusses using teaching-learning-based optimization. Int. J. Optim. Civil Eng. 2013, 3, 431–444.
59. Dehghani, M.; Mashayekhi, M.; Salajegheh, E. Topology optimization of double- and triple-layer grids using a hybrid methodology. Eng. Optim. 2015, 48, 1333–1349. [CrossRef]
60. Camp, C.V.; Bichon, B.J.; Stovall, S.P. Design of steel frames using ant colony optimization. J. Struct. Eng. 2005, 131, 369–379. [CrossRef]
61. Aldwaik, M.; Adeli, H. Advances in optimization of highrise building structures. Struct. Multidiscip. Optim. 2014, 50, 899–919. [CrossRef]
62. Bekdas¸, G.; Nigdeli, S.M.; Yang, X.-S. Sizing optimization of truss structures using flower pollination algorithm. Appl. Soft Comput. 2015, 37, 322–331. [CrossRef]
63. Dede, T.; Ayvaz, Y. Combined size and shape optimization of structures with a new meta-heuristic algorithm. Appl. Soft Comput. 2015, 28, 250–258. [CrossRef]
64. Lieu, Q.X.; Do, D.T.; Lee, J. An adaptive hybrid evolutionary firefly algorithm for shape and size optimization of truss structures with frequency constraints. Comput. Struct. 2018, 195, 99–112. [CrossRef]
65. Faramarzi, A.; Afshar, M. Application of cellular automata to size and topology optimization of truss structures. Sci. Iran. 2012, 19, 373–380. [CrossRef]
66. Degertekin, S.; Lamberti, L.; Ugur, I. Discrete sizing/layout/topology optimization of truss structures with an advanced Jaya algorithm. Appl. Soft Comput. 2019, 79, 363–390. [CrossRef]
67. Kazakis, G.; Kanellopoulos, I.; Sotiropoulos, S.; Lagaros, N.D. Topology optimization aided structural design: Interpretation, computational aspects and 3D printing. Heliyon 2017, 3, e00431. [CrossRef]
68. Fraternali, F.; Marino, A.; Sayed, T.E.; Cioppa, A.D. On the structural shape optimization through variational methods and evolutionary algorithms. Mech. Adv. Mater. Struct. 2011, 18, 225–243. [CrossRef]
69. Shimoda, M.; Kameyama, K.; Shi, J.-X. Tailoring static deformation of frame structures based on a non-parametric shape–size optimization method. Int. J. Solids Struct. 2017, 112, 143–154. [CrossRef]
70. Sotiropoulos, S.; Kazakis, G.; Lagaros, N.D. High performance topology optimization computing platform. Procedia Manuf. 2020, 44, 441–448. [CrossRef]
71. Mortazavi, A.; Tog˘ an, V. Sizing and layout design of truss structures under dynamic and static constraints with an integrated particle swarm optimization algorithm. Appl. Soft Comput. 2017, 51, 239–252. [CrossRef]
72. Richardson, J.N.; Adriaenssens, S.; Bouillard, P.; Coelho, R.F. Multiobjective topology optimization of truss structures with kinematic stability repair. Struct. Multidiscip. Optim. 2012, 46, 513–532. [CrossRef]
73. Hosseini, S.S.; Hamidi, S.A.; Mansuri, M.; Ghoddosian, A. Multi Objective Particle Swarm Optimization (MOPSO) for size and shape optimization of 2D truss structures. Period. Polytech. Civil Eng. 2015, 59, 9–14. [CrossRef]
74. Zavala, G.R.; Nebro, A.J.; Durillo, J.J.; Luna, F. Integrating a multi-objective optimization framework into a structural design software. Adv. Eng. Softw. 2014, 76, 161–170. [CrossRef]
75. Loógoó, J.N.; Ismail, H. Milestones in the 150-year history of topology optimization: A review. Comput. Assist. Methods Eng. Sci. 2020, 27, 97–132.
76. Kuhn, H.; Tucker, A. Nonlinear programming. In Proceedings of the 2nd Berkeley Symposium, Berkeley, CA, USA, 31 July–12 August 1950; University of California Press: Berkeley, CA, USA, 1951.
77. Khot, N.; Berke, L. Structural Optimization Using Optimality Criteria Methods; NTRS: Chicago, IL, USA, 1984.
78. Rao, S.S. Engineering Optimization: Theory and Practice; John Wiley & Sons: Hoboken, NJ, USA, 2019.
79. Dobbs, M.W.; Felton, L.P. Optimization of Truss Geometry. J. Struct. Div. 1969, 95, 2105–2118. [CrossRef]
80. Sigmund, O. On the usefulness of non-gradient approaches in topology optimization. Struct. Multidiscip. Optim. 2011, 43, 589–596. [CrossRef]
81. Ganjefar, S.; Tofighi, M. Optimization of quantum-inspired neural network using memetic algorithm for function approximation and chaotic time series prediction. Neurocomputing 2018, 291, 175–186. [CrossRef]
82. Yuan, Y.; Zhang, R.; Hu, R.; Ruan, X. Prediction of CCR5 receptor binding affinity of substituted 1-(3, 3-diphenylpropyl)- piperidinyl amides and ureas based on the heuristic method, support vector machine and projection pursuit regression. Eur. J. Med. Chem. 2009, 44, 25–34. [CrossRef] [PubMed]
83. Yang, X.-S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010.
84. Lee, K.Y.; El-Sharkawi, M.A. Modern Heuristic Optimization Techniques: Theory and Applications to Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2008; Volume 39.
85. Goldberg, D.E.; Holland, J.H. Genetic Algorithms and Machine Learning; Addison-Wesley Professional: Boston, MA, USA, 1988.
86. Geem, Z.W.; Kim, J.H.; Loganathan, G.V. A new heuristic optimization algorithm: Harmony search. Simulation 2001, 76, 60–68. [CrossRef]
87. Yang, X.S.; He, X. Firefly algorithm: Recent advances and applications. Int. J. Swarm Intell. 2013, 1, 36–50. [CrossRef]
88. Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization; Technical report-tr06; Engineering Faculty, Computer, Erciyes University: Kayseri, Turkey, 2005.
89. Storn, R.; Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [CrossRef]
90. Glover, F. Tabu Search—Part I. ORSA J. Comput. 1989, 1, 190–206. [CrossRef]
91. Rao, V.R.; Savsani, V.J.; Vakharia, D. Teaching–learning-based optimization: A novel method for constrained mechanical design optimization problems. Comput. Aided Des. 2011, 43, 303–315. [CrossRef]
92. Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995.
93. Yang, X.-S. A New Metaheuristic Bat-Inspired Algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74.
94. Yang, X.-S.; Deb, S. Cuckoo Search via Lévy Flights. In Proceedings of the 2009 World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009.
95. Rao, R. Jaya: A simple and new optimization algorithm for solving constrained and unconstrained optimization problems. Int. J. Ind. Eng. Comput. 2016, 7, 19–34.
96. Beheshti, Z.; Shamsuddin, S.M.H. A review of population-based meta-heuristic algorithms. Int. J. Adv. Soft Comput. Appl. 2013, 5, 1–35.
97. Kociecki, M.; Adeli, H. Two-phase genetic algorithm for topology optimization of free-form steel space-frame roof structures with complex curvatures. Eng. Appl. Artif. Intell. 2014, 32, 218–227. [CrossRef]
98. Cheng, M.Y.; Prayogo, D.; Wu, Y.W.; Lukito, M.M. A Hybrid Harmony Search algorithm for discrete sizing optimization of truss structure. Autom. Constr. 2016, 69, 21–33. [CrossRef]
99. Arjmand, M.; Azqandi, M.S.; Delavar, M. Hybrid improved dolphin echolocation and ant colony optimization for optimal discrete sizing of truss structures. J. Rehabil. Civil Eng. 2018, 6, 70–87.
100. Cao, H.; Qian, X.; Chen, Z.; Zhu, H. Enhanced particle swarm optimization for size and shape optimization of truss structures. Eng. Optim. 2017, 49, 1939–1956. [CrossRef]
101. Aoues, Y.; Chateauneuf, A. Benchmark study of numerical methods for reliability-based design optimization. Struct. Multidiscip. Optim. 2010, 41, 277–294. [CrossRef]
102. Lopez, R.H.; Beck, A.T. Reliability-based design optimization strategies based on FORM: A review. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 506–514. [CrossRef]
103. Goswami, S.; Chakraborty, S.; Chowdhury, R.; Rabczuk, T. Threshold shift method for reliability-based design optimization. Struct. Multidiscip. Optim. 2019, 60, 2053–2072. [CrossRef]
104. Talaslioglu, T. Design optimisation of dome structures by enhanced genetic algorithm with multiple populations. Sci. Res. Essays 2012, 7, 3877–3896.
105. Baghlani, A.; Makiabadi, M.; Rahnema, H. A new accelerated firefly algorithm for size optimization of truss structures. Sci. Iran. 2013, 20, 1612–1625.
106. Kaveh, A.; Ghazaan, M.I. Layout and size optimization of trusses with natural frequency constraints using improved ray optimization algorithm. Iran. J. Sci. Technol. Trans. Civil Eng. 2015, 39, 395.
107. Maheri, M.R.; Askarian, M.; Shojaee, S. Size and topology optimization of trusses using hybrid genetic-particle swarm algorithms. Iran. J. Sci. Technol. Trans. Civil Eng. 2016, 40, 179–193. [CrossRef]
108. Kaveh, A.; Moradveisi, M. Size and Geometry Optimization of Double-Layer Grids Using CBO and ECBO Algorithms. Iran. J. Sci. Technol. Trans. Civil Eng. 2017, 41, 101–112. [CrossRef]
109. AlHamaydeh, M.; Barakat, S.; Nasif, O. Optimization of support structures for offshore wind turbines using genetic algorithm with domain-trimming. Math. Probl. Eng. 2017, 5978375. [CrossRef]
110. Kaveh, A. Sizing optimization of skeletal structures using the enhanced whale optimization algorithm. In Applications of Metaheuristic Optimization Algorithms in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 47–69.
111. Kaveh, A.; Behnam, A. Design optimization of reinforced concrete 3D structures considering frequency constraints via a charged system search. Sci. Iran. 2013, 20, 387–396.
112. Arayici, Y.; Fernando, T.; Munoz, V.; Bassanino, M. Interoperability specification development for integrated BIM use in performance based design. Autom. Constr. 2018, 85, 167–181. [CrossRef]
113. Sotiropoulos, S.; Lagaros, N.D. Topology Optimization of Framed Structures using SAP2000. Procedia Manuf. 2020, 44, 68–75. [CrossRef]
114. Zhou, S.; Cadman, J.; Chen, Y.; Li, W.; Xie, Y.M.; Huang, X.; Appleyard, R.; Sun, G.; Li, Q. Design and fabrication of biphasic cellular materials with transport properties—A modified bidirectional evolutionary structural optimization procedure and MATLAB program. Int. J. Heat Mass Transf. 2012, 55, 8149–8162. [CrossRef]
115. Zegard, T.; Paulino, G.H. GRAND3—Ground structure based topology optimization for arbitrary 3D domains using MATLAB. Struct. Multidiscip. Optim. 2015, 52, 1161–1184. [CrossRef]
116. Marler, R.T.; Arora, J.S. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [CrossRef]
117. Coello Coello, C.A.; van Veldhuizen, D.A.; Lamont, G.B. Multi-Criteria Decision Making. In Evolutionary Algorithms for Solving Multi-Objective Problems; Springer: Boston, MA, USA, 2002; pp. 321–347.
118. Athan, T.W.; Papalambros, P.Y. A note on weighted criteria methods for compromise solutions in multi-objective optimization. Eng. Optim. 1996, 27, 155–176. [CrossRef]
119. Zadeh, L. Optimality and non-scalar-valued performance criteria. IEEE Trans. Autom. Control 1963, 8, 59–60. [CrossRef]
120. Sanaei, E.; Babaei, M. Topology optimization of structures using cellular automata with constant strain triangles. Int. J. Civil Eng. 2012, 10, 179–188.
121. Chamoret, D.; Qiu, K.; Domaszewski, M. Optimization of truss structures by a stochastic method. Int. J. Simul. Multidiscip. Des. Optim. 2009, 3, 321–325. [CrossRef]
122. Kaveh, A. Optimum design of castellated beams using the tug of war algorithm. In Applications of Metaheuristic Optimization Algorithms in Civil Engineering; Springer: Berlin/Heidelberg, Germany, 2017; pp. 9–30.
123. Sharafi, P.; Hadi, M.N.; Teh, L.H. Geometric design optimization for dynamic response problems of continuous reinforced concrete beams. J. Comput. Civil Eng. 2014, 28, 202–209. [CrossRef]
124. Kravanja, S.; Žula, T.; Klanšek, U. Multi-parametric MINLP optimization study of a composite I beam floor system. Eng. Struct. 2017, 130, 316–335. [CrossRef]
125. Kravanja, S.; Turkalj, G.; Šilih, S.; Žula, T. Optimal design of single-story steel building structures based on parametric MINLP optimization. J. Constr. Steel Res. 2013, 81, 86–103. [CrossRef]
126. Jelusic, P.; Kravanja, S. Optimal design of timber-concrete composite floors based on the multi-parametric MINLP optimization. Compos. Struct. 2017, 179, 285–293. [CrossRef]
127. Bussieck, M.R.; Pruessner, A. Mixed-integer nonlinear programming. SIAG OPT Newsl. Views News 2003, 14, 19–22.
128. Kaveh, A.; Hamedani, K.B.; Hosseini, S.M.; Bakhshpoori, T. Optimal design of planar steel frame structures utilizing meta- heuristic optimization algorithms. In Structures; Elsevier: Amsterdam, The Netherlands, 2020.